Rust Decay Calculator: Exponential Decay Model

Purpose of the Rust Decay Calculator

This template models material degradation over time using standard exponential decay formulas. It allows users to simulate the reduction of physical properties, such as material thickness or structural strength, based on specific half-life inputs.

• Models degradation: Applies exponential mathematics to track how materials lose integrity over time.
• Simulates reduction: Projects the decline of properties based on user-defined half-life parameters.
• Calculates specifics: Determines precise decay constants and remaining fractions for specific time points.
• Visualizes results: Maps the relationship between absolute property values and the percentage of material remaining on a dual-axis chart.
• Versatile utility: Functions effectively as a rust decay rate calculator for gaming mechanics or educational physics scenarios.

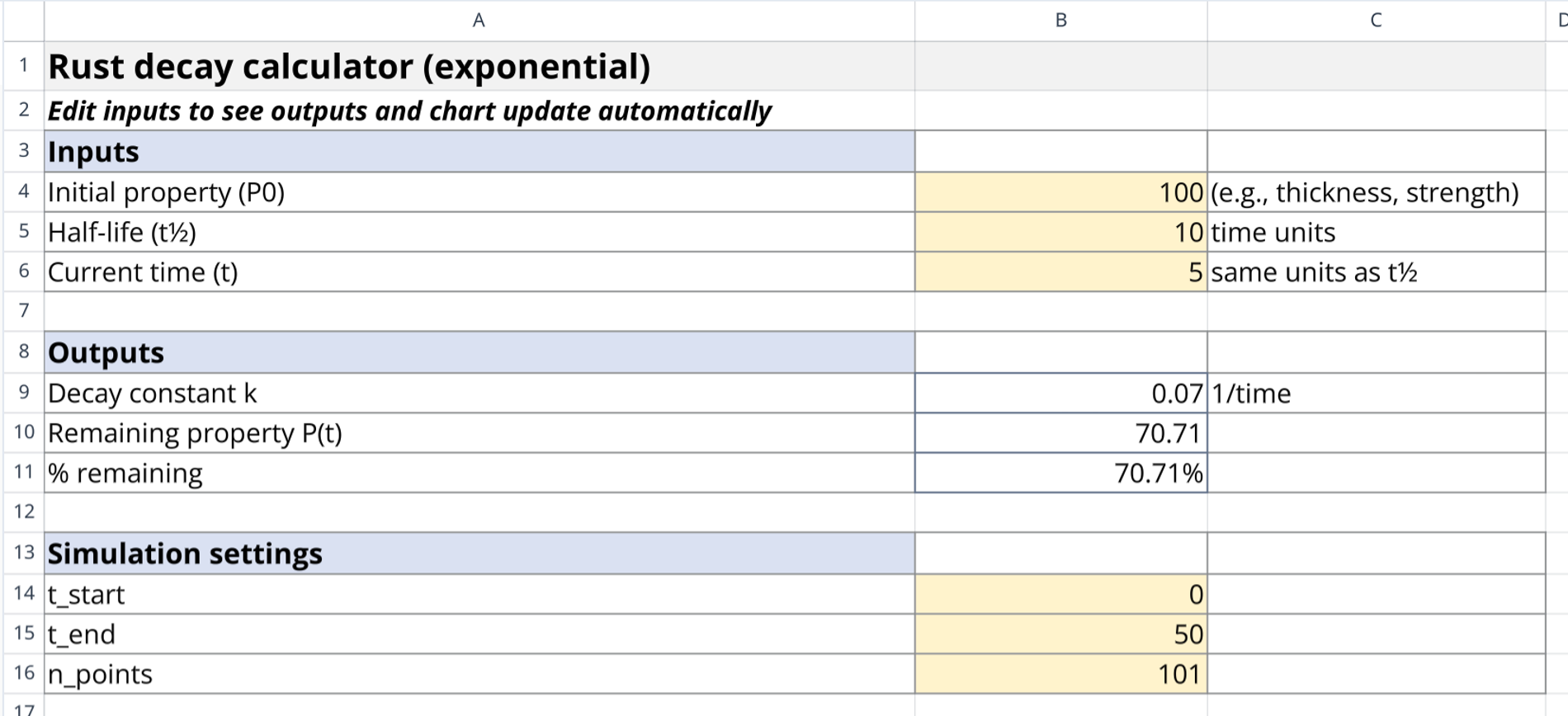
Input parameters and simulation settings

The template is controlled by a set of input variables located in the top-left region of the sheet. These parameters define both the physical properties of the material and the scope of the simulation.

• Initial Property Value ($P_0$): Sets the starting material strength, health, or thickness (defaulting to 100).
• Half-Life ($t_{1/2}$): Defines the duration required for the property to reduce to exactly half of its initial value.
• Target Time ($t$): Specifies a distinct moment in time for an instantaneous calculation of remaining material.
• Simulation Range: Controls the start time ($t_{start}$) and end time ($t_{end}$) to define the window of observation.
• Resolution: Determines the number of data points ($n_{points}$) generated, ensuring the rust decay time calculator logic produces a smooth curve.

Calculation logic and Python integration

The core mathematical operations are handled by a Python script embedded directly in the Python spreadsheet. This script reads the input cells and uses the NumPy library to perform vectorised calculations.

• Decay Constant: Python computes the constant $k = \ln(2)/t_{1/2}$ automatically based on the user's half-life input.
• Time-Series Generation: The script uses numpy.linspace to create an array of time values spanning from the start to the end parameters.
• Exponential Formula: It applies the function $P(t) = P_0 \times e^{-kt}$ to every point in the generated time array simultaneously.
• Data Structure: The output is organized into a decay calculator rust simulation table containing 101 distinct data points.
• Automatic Updates: The Python DataFrame recalculates instantly whenever any input cell is modified, ensuring data consistency.

Visualizing decay data

A second Python cell reads the generated simulation table to construct a detailed visualization. This chart helps users correlate absolute values with relative percentages.

• Chart Type: Generates a dual-axis Plotly line chart derived directly from the simulation DataFrame.
• Primary Axis: The left y-axis displays the absolute property value ($P(t)$) as it decreases over time.
• Secondary Axis: The right y-axis shows the percentage of material remaining on a 0-100% scale.
• Formatting: Includes a horizontal legend and light gridlines to ensure the data is easy to read and interpret.
• Interactivity: The curve trajectory updates immediately when rust decaying calculator parameters are adjusted, allowing for rapid scenario testing.

Who this Rust Decay Calculator template is for

This tool is designed for users who need to model degradation without building complex formulas manually.

• Gamers: Players looking for a rust base decay calculator or rust door decay calculator to optimize structure maintenance and track durability.
• Students: Learners studying exponential decay models, logarithms, and half-life concepts in physics or math.
• Engineers: Professionals requiring a quick method to model theoretical material loss or rust decay calculator wall integrity.
• Data Analysts: Users demonstrating how to integrate Python-based mathematical modeling within a familiar spreadsheet interface.

Use Quadratic to Model Material Degradation with Exponential Decay

• Model material degradation accurately with built-in exponential decay formulas.
• Define initial property values, half-life, and simulation time ranges in a single interface.
• Automate complex decay constant and time-series calculations using embedded Python.
• Visualize both absolute property values and remaining percentages on an interactive dual-axis chart.
• Instantly see results update and test various degradation scenarios by adjusting inputs.
• Utilize for diverse applications like gaming mechanics, educational physics, or engineering material loss.

Duplicate this Rust Decay Calculator file